kalkulatu poligono honen azalera irudia bi poligonotan deskonpola daiteki:abz triangelua da cdef trzezioa
abc triangeluaren azalera=12-9.9
2
abc triangeluaren azalera=12-9.9
2
2013(e)ko maiatzaren 27(a), astelehena
irudi korporatobo
Irudi korporatibo
Marketinean, enpresa edo beste erakunde baten irudi korporatiboa gizarteak erakunde hori ikusten duen modua da. Irudi korporatiboa eragiten duten faktoreak anitz dira: produktua,bezeroekiko eta hornitzaileekiko harremanak, komunikazioa, gizarte erantzukizuna, lan giroa, eraikina etab. Faktore hauen guztien bitartez enpresak irudi bateratu eta garbia erakutsi nahi duenean, irudi korporatibo osatzen ari dela esaten da. Horretarako, enpresa identitate korporatibotik, enpresa benetan den horretatik alegia, abiatu eta gizartera bidaltzen dituen mezuak identitate horretara egokitu behar ditu. Hori dela eta, irudi korporatiboan bereziki zaintzen dira elementu grafikoak, hala nola logotipoa, baina baita ere koloreak eta agirietan erabilitako tipografia non, noiz eta nola agertu behar diren. Horietaz haraindi, irudi korporatiboak bezeroen arreta, langileen harrera eta bestelako arloak zaindu beharko ditu, enpresa modu argi eta zuzen batez identifikatua izan dadin. Horretarako guztirako, erakundeek arloz arloko eskuliburuak osatzen dituzte, non irudi egokia emateko ezarri diren elementuak zehazten diren.
zirkuluaren azalera
Azalera
Azalera gainazal baten neurria da, hau da, irudi geometriko batek betetzen duen plano-zatiaren hedadura.
Geografian, lurraldeen luze-zabala adierazteko eremu erabiltzen da.
poligono erregularrearen azalera
Poligono erregular
Geometrian, poligono bat erregularra da, aldeberdina (alde guztiak luzera berekoak dira) eta angeluberdina (angelu guztiak neurri
berekoak dira) bada.
Poligono erregularrak bi motatakoak izan daitezke: ganbilak eta ahurrak (izar itxurakoak azken horiek, izar-poligono izenekoak).
Hiru eta lau aldeko poligono erregularrak hiruki aldeberdina eta karratua dira, hurrenez hurren; alde gehiagoko poligono erregularrak izendatzeko, erregular terminoa gehitzen da (pentagono erregularra, hexagono erregularra...).
2013(e)ko maiatzaren 23(a), osteguna
poligono eregulrraren azalra
poligonoaren azalera triangulu horietrako batean azalera bider pligonoen al konpurua da.
trapezioen azalera
B oinarria handiako b oinarri txikiko eta h altuerako bi traperzo berdin elkartuz (B b oinarriko eta h altuerako erronboide lortzen da.
triangeluaren azalera
Triangeluar azalera
Orrialde hau ez dago datu-basean; artikulua hastea nahi baduzu, testu leihoan idatzi dezakezu (Mesedez, zure lehen bisita bada, irakurri lehenik eta behin Laguntza orrialdea). Hona nahi gabe heldu bazara, zure nabigatzaileko atzera botoia sakatu.
Oharra: Ez duzu saioa hasi.
2013(e)ko maiatzaren 21(a), asteartea
Trapezio
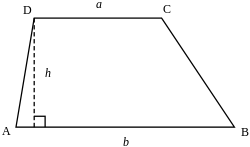
| Trapezioa | |
|---|---|
 Trapezioak: zuzena, isoszelea eta eskalenoa. | |
| Mota | Laukia |
| Aldeak | 4 |
| Azalera |  |
| Propietateak | ganbila |
Trapezioa bi alde paralelo, oinarriak deiturikoak, baino ez dituen laukia da. Oinarrien arteko distantziari garaiera deritzo.
Trapezioaren A azalera, a eta b bi oinarrien baturaerdiaren eta h garaieraren arteko biderkadura da
triangeluaren azalera
TRIANGELUAREN AZALERA
b oinarriko eta h altuerako triangeluaren azalela b oinarriko eta h altuerako erronboidearen azaleraren erdia da.
b oinarriko eta h altuerako triangeluaren azalela b oinarriko eta h altuerako erronboidearen azaleraren erdia da.
paralelogramoen azalera
Paralelogramoen azalera
| Paralelogramoa | |
|---|---|
 Lau paralelogramo mota | |
| Mota | Laukia |
| Aldeak | 4 |
| Simetria-taldea | C2, [2]+, (22) |
| Azalera | b × h; ab sin θ |
| Propietateak | ganbila |
Paralelogramoa aurrez aurreko aldeak paraleloak eta berdinak dituen laukia da.
Paralelogramoaren azalera oinarria bider garaiera biderkatuz kalkulatzen da.
Esate baterako, b neurtzen duten bi alde paralelo h garaieraz aldendurik badira,
paralelogramo horren azalera b bider h eginez ateratzen da;
era berean, beste bi alde paraleloek a luzera badute, eta alboko aldearekin eratzen duen angelua ß bada,
azalera a bider b bider sinu ß biderkatuz kalkulatzen da.
perimetroa
Perímetro
En matemáticas, el perímetro es la suma de las longitudes de los lados de una figura geométrica.
2013(e)ko maiatzaren 20(a), astelehena
2013(e)ko maiatzaren 14(a), asteartea
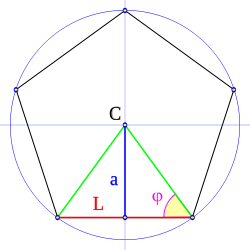
Zer da zirkunferentzia?
Zirkunferentzia, geometria euklidearrean, puntu jakin batetik distantzia berera dauden puntuen multzoa da. Puntu horri , Zentro edo foku deritzo. Zentrotik zirkunferentziaren puntuetara dagoen distantziari erradio esaten zaio eta zentrotik pasa eta zirkunferentziak mugatzen duen zuzenkiaren luzerari berriz, diametro. Zirkunferentziaren perimetroak mugatzen duen azalerari zirkulu deritzo.
 |
Zirkunferentzia
Zirkunferentzia, geometria euklidestarrean, puntu jakin batetik distantzia berera dauden puntuen multzoa da. Puntu horri, zentro edo fokuesaten zaio. Zentrotik zirkunferentziaren puntuetara dagoen distantziari erradio deritzo. Zentrotik pasa eta zirkunferentziak mugatzen duen zuzenkiaren luzerari diametro deritzo.
Zirkunferentziaren perimetroak mugatzen duen azalerari zirkulu deritzo.
2013(e)ko maiatzaren 13(a), astelehena
Zirkunferentzia
Zirkunferentzia, geometria euklidestarrean, puntu jakin batetik distantzia berera dauden puntuen multzoa da. Puntu horri, zentro edo fokuesaten zaio. Zentrotik zirkunferentziaren puntuetara dagoen distantziari erradio deritzo. Zentrotik pasa eta zirkunferentziak mugatzen duen zuzenkiaren luzerari diametro deritzo.
Zirkunferentziaren perimetroak mugatzen duen azalerari zirkulu deritzo.
Paralelogramoa aurrez aurreko aldeak paraleloak eta berdinak dituen laukia da.
Paralelogramoaren azalera oinarria bider garaiera biderkatuz kalkulatzen da. Esate baterako, b neurtzen duten bi alde paralelo h garaieraz aldendurik badira, paralelogramo horren azalera b bider h eginez ateratzen da; era berean, beste bi alde paraleloek a luzera badute, eta alboko aldearekin eratzen duen angelua ß bada, azalera a bider b bider sinu ß biderkatuz kalkulatzen da.
[aldatu]Paralelogramoaren legea
Paralelogramoaren legea izeneko lege bat dago, ondorengo formulaz definitua:
Lauki-motak
- Lauki ganbilak: barne angelu guztiak 180º baino txikiagoak dira (erpin guztiak kanpora).
- Paralelogramoa: aurrez aurreko aldeak paraleloak dituena. Horren ondorioz, aurrez aurreko aldeak eta angeluak ere berdinak dira. Haien adibide batzuk:
- Karratua: lau aldeak berdinak eta lau angeluak zuzenak dituena.
- Laukizuzena: lau angelu zuzen eta aurrez aurreko aldeak berdinak dituena.
- Erronboa: lau aldeak berdinak dituen baina angelu zuzenik ez duena.
- Erronboidea: aurrez aurreko aldeak soilik berdinak dituen eta angelu zuzenik ez duena.
- Trapezioa: soilik bi alde paralelo dituena. Hiru mota daude:
- Trapezio zuzena: bi angelu zuzen ditu.
- Trapezio isoszelea: paraleloak ez diren aldeak luzera berdinekoak dira.
- Trapezio eskalenoa: paraleloak ez diren aldeak luzera desberdinekoak dira.
- Trapezoide: elkarren arteko alde bakarra.
- Paralelogramoa: aurrez aurreko aldeak paraleloak dituena. Horren ondorioz, aurrez aurreko aldeak eta angeluak ere berdinak dira. Haien adibide batzuk:
Harpidetu honetara:
Mezuak (Atom)